什么是数据拟合
数据拟合又称曲线拟合,俗称拉曲线,是一种把现有数据透过数学方法来代入一条数式的表示方式。科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合(fitting)。
举个简单拿到例子,函数y=x(x属于R);每一个x的值都有一个y值。假设需要采样某个器件在不同种条件下得到不同种的值,就好比在自变量x下得到得到应变量y。当无法采样时,该如何,这个时候就在这些数据中找规律。一旦规律找出来,就可以在无法采样时找到这个值。当然,这个时候这个值并不准确,当采样的数据越多,那么在曲线规律下值就越准确,这样在曲线规律预测的这个值就更加精确实际测量到的值,这就是数据拟合。
数据拟合的意义
数据拟合在很多地方都有着重大意义。比如预测,估算。总的来说有以下两点:
- 总结事件发生的规律
- 规律属于何种
本文数据拟合的意义在于实现智能小车在墙迷宫走迷宫时,将传感器接收到的数据经过数据拟合得到墙壁与传感器的距离进行判断实现循迹和判断迷宫路口,那么首先应该实现红外传感器接收到的值和距离进行数据拟合。
传感器值与距离的数据拟合
红外线传感器工作原理
首先,实现传感器值与距离的数据拟合是为了CPU读取了传感器的值,从而知道自己所在的位置,以便于CPU准确的做出下一步指令。传感器的值是如何获取的呢?这里大致解释一下红外线的工作原理。
红外线由两部分构成,接收管和发射管。发射管接通电源后,发射红外线。当障碍物的位置不同,反射的红外线大小也不同,当然障碍物的颜色也对红外线反射有影响。反射的红外线将会被传感器的接收管检测到。而接收管类似于变阻器,不过电阻的大小由反射红外线大小控制;而电阻的大小我们不能检测到,但可以检测到接收管的电压。因此看电压的大小可以知道反射红外线的大小。。当然如果没有障碍物时,接收管就无法接收到反射的红外线。
红外传感器函数公式
红外传感器有一个函数公式,logv = clogr + d。这里的公式本文不做解释,后期向大家介绍。
最小二乘法
本文使用最小二乘法求出c,d的值。那么什么是最小二乘法?
最小二乘法,是一种数学优化方法。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便的求得未知的数据,并使得求得的数据与实际数据之间误差的平方和为最小。
理解
从函数微积分角度:
假设某次实验得到了四个数据点(x, y):(1,6)、(2,5)、(3,7)、(4,10),我们希望找出一条和这四个点最匹配的直线 y=a+bx,即找出在某种“最佳情况”下能够大致符合如下超定线性方程组的a和b:
a + 1b = 6;
a + 2b = 5;
a + 3b = 7;
a + 4b = 10;
最小二乘法就是求出(6-(a + 1b))^2+((5-(a + 2b))^2+(7-(a + 3b))^2+(10-(a + 4b))的最小值。那我们就设最小值为z,则:
z=(6-(a + 1b))^2+((5-(a + 2b))^2+(7-(a + 3b))^2+(10-(a + 4b));
因为平方了,因此z恒大于等于0。同时可以知道,z是不可能达到最大值的(只要足够偏离的话,那肯定是越来越大的), 我们可以看图,如图1-1所示,当蓝色的线上下移动旋转,绿色只有最小值,没有最大值。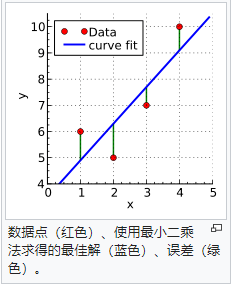
那该如何求z呢?一种就是找出a与b的等式替换其中一个。这个不仅麻烦,而且在这里找不到a和b的等式。第二种方式就是通过对z分别求a和b的偏导数,然后使他们等于零得到。
0 = 8a + 20b - 56;
0 = 20a + 60b - 154;
两者联立求出a = 3.5 , b = 1.4,得出最匹配的直线为 y = 3.5 + 1.4x。
为什么要等于零。z是一个多元函数,从几何上看,z是一个曲面,由于z恒大于等于零,z类似于如图1-2所示的曲面图。而在数学中,一个多变量的函数的偏导数(英语:partial derivative)是它关于其中一个变量的导数,而保持其他变量恒定。因此两个偏导数要同时等于0才能求出z最小值。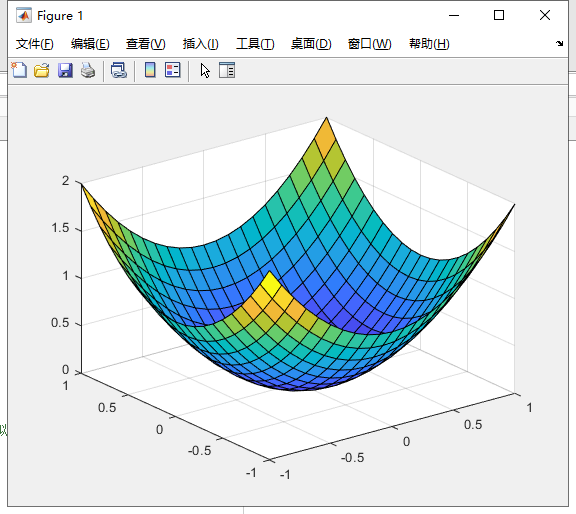
从线性代数角度:
这边就不介绍了,下面是这方面的资料和视频:
- 最小二乘法的线性代数证明
- 最小二乘法——百度百科
最终我们可以知道最小二乘法公式为: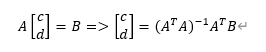
实验测量值
| 距离 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|
| 电压值 | 2.7 | 1.8 | 1.3 | 1 | 0.74 | 0.58 |
| 距离 | 9 | 10 | 11 | 12 | 13 | 14 |
| 电压值 | 0.47 | 0.38 | 0.33 | 0.28 | 0.24 | 0.2 |
矩阵形式为:
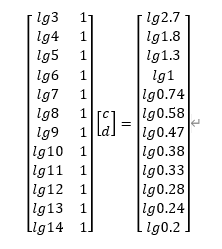
代码
下面的代码就是使用最小二乘法求出从从c,d:
% 定义域 r1
r1 = 3:14;a
% 区间 v
vo1 = [2.7 1.8 1.3 1 0.74 0.58 0.47 0.38 0.33 0.28 0.24 0.2];
% r1的矩阵
A1 = [log10(r1);ones(1,12)]';
% v1的矩阵
v1 = log10(vo1);
% v = c*log10(r) + d ,c,d值
ans_cd1 = inv(A1'*A1)*A1'*v1';
fprintf('ans_cd1 = %g\n',ans_cd1);最后用matlab将图形表示出来:
x = 3:0.01:14;
y = 10.^(-1.70104*log10(x)+1.28584);
plot(r1,vo1 ,'green-o',x,y,'r');
xlabel('距离');
ylabel('电压值');
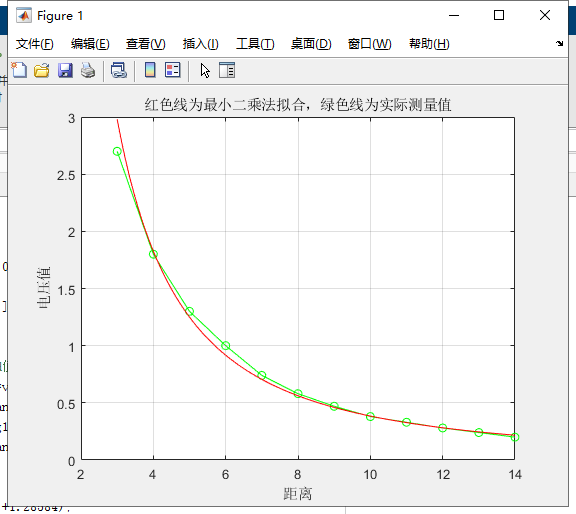
title('红色线为最小二乘法拟合,绿色线为实际测量值');
grid on图3-1为红外线传感器值与距离的数据拟合图。